|
|
BEAM From the Ground Up is a BEAM Reference Library site.
Nv neurons and Nv nets
What they are, what they
do
On this page, we'll tackle two challenging topics -- Nv neurons (the building block of advanced BEAM circuits), and Nv nets (networks of Nv Neurons, designed to do our bidding).
The Nv ("nervous") neuron --
the basics
Let's start with the basics -- a single "Nv
neuron"
(a.k.a., a "Nervous neuron",
or "Nv"
for short). There are a number of varieties
of this basic circuit, but the simplest and most-common form
looks like this:
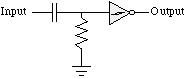
This forms a "differentiating element" in a circuit (since the input is coupled via a capacitor, it responds to changes in input voltage, rather than the input voltage per se), and it consists of just 3 elements -- a capacitor, a resistor, and an inverter.
With Vcc = 5 Volts, let's say the input switches from 0 Volts to +5 Volts. A positive rising voltage transition is applied to the Nv capacitor input. The voltage on the other side of the Nv capacitor and across the resistor at the Nv inverter input will rise instantaneously to +5 V. With the Nv inverter input at +5V, the Nv inverter output drops to 0 volts in a matter of a few nanoseconds. If the capacitor input remains high, the voltage on the inverter input will immediately start to decay exponentially towards 0 volts as the capacitor discharges. During this time the voltage across the capacitor increases while the voltage across the resistor drops. At some point, the voltage at the Nv inverter input will cross the switching threshold, the Nv "times out" and Nv inverter output switches back to +5V thereby generating a positive voltage transition.
We assume that the slowly changing waveform at the Nv input produces a single output transition when it crosses the Nv switching threshold. This is accomplished by using a 74HC14 or similar CMOS Schmitt trigger. When 74HC04 or 74HC240s are used for Nv inverters some nasty oscillations occur during switching which makes these inverters unsuitable for most Nv networks greater than 2 Nv in series.
While the output voltage of an Nv neuron will fluctuate with time (and as a function of its input voltage), the two states we are most concerned with are (1) when the output voltage is "high" (at or near the circuit's supply voltage, Vcc), and (2) when the output voltage is "low" (at or near the circuit's ground). For reasons lost in the mists of time, Nv neurons (and the circuits built from them) are described in terms of negative logic, and so Nv neurons are deemed to be active when their output voltage is "low."
If you're experienced with electronics, you'll notice something odd about the above circuit -- namely, that it shouldn't work! In theory this circuit shouldn't work without an extra pair of diodes connected to the inverter input. However, all modern CMOS IC families (C, HC, AC, etc) have those diodes built in for static protection; by using CMOS chips for our creations, we'll be covered.
The CMOS protective input diodes play an important role in resetting the charge on the Nv input capacitor to 0 volts prior to the next positive transition. This occurs when an Nv input drops to 0 volts. This negative voltage transition is capacitively coupled to the inverter input where the protective input diode clamps the input voltage to -0.6 V. This means the charge across the capacitor is nearly 0 volts and ensures a repeatable Nv time out period when the input is driven positive.
This is all OK, as far as it goes. To make things more interesting, let's hook up a second Nv neuron:
Connecting Nv neurons -- Nv networks
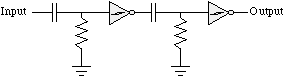
Now, if you step the input from 0 to 5 Volts, the first neuron's output will drop to 0 Volts (this neuron is now "on"); this transition will rapidly drain the second neuron's capacitor, resulting (after a delay) in a 5 Volt output from it (the second neuron is now "off").
If the input voltage is now dropped back to 0 Volts, the first neuron's capacitor will drain, resulting (after a very short delay) in a 5 Volt output (the first neuron is now "off"). This will cause the second neuron's capacitor to charge, and (after a short delay) we will see a 0 Volt output from it (the second neuron is now "on").
You can keep at this, adding neuron to neuron, eventually tying the output of the last neuron to the input of the first. This ring of Nv neurons is just one type of Nv Net, although more complex networks have been built.
Nv Nets generate square waves with varying duty cycles from each Nv neuron, like this:
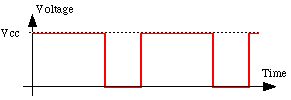
Again, Nv neurons use negative logic, so in this graph, "on" is denoted by low (essentially zero) voltage, and "off" is denoted by high voltage (Vcc, usually 3 - 5 volts). Each Nv neuron is generating its own square wave; the duty cycles and phasing between the neurons' waves is determined by the details of how the circuitry is interconnected. This behavior can be used to drive a number of devices (but more on that later).
Meanwhile, as things are left running, the little "on" (low) wave moves around the Nv net. This wave essentially takes on a life of its own, and is often called a Process. Note that depending on your net's initialization circuitry, you can have one or more active processes running around in it. The native state for a "raw" Nv Net at powerup is saturation -- here, there are half as many active processes as there are Nvs (alternate Nvs are active at any given time). Depending on your application, this may be what you want, or you may want to have initialization circuitry that reduces this mele to a single active process.
Where to go next
If you're new to Nv
networks, I'd suggest you take the subservient pages in
turn:
You can do a lot of interesting things with just 2 Nvs. The bicore discusses the various flavors of 2-Nv circuits.The quadcore discusses the most commonly-used 4-Nv net configuration (a big loop).
Once you get beyond simple loops of Nvs, you'll need to know more about how to hook groups of Nvs together; I've got some material on that in a page on Nv net connections and topology.
Applications discusses how to actually use an Nv net in your projects, and what sorts of projects can be built with them.
Once you get past Nv nets of 2 or 3 Nvs, you'll need to worry about how the circuit will start running when you apply power. This means you'll have to learn about the various kinds (some simple, some not so simple) of Nv net initialization circuitry.
As your creations get more complex, you'll want to change your Nv net's behavior -- based, say, on sensor data, or some remote control. For this, you'll need to learn about influencing your Nv Net.
When you've got all this down pat, you'll want to learn about all the various variants of Nvs (since the discussion to this point just talks about "vanilla" Nvs). I've got a section on Nv variants to round out your education.
|
|
|
|
|
|
||
|
|
This page was last updated on |
|
